A computer can only understand binary numbers, as we all know. All that exists is a lengthy sequence of 1s and 0s: every word in this text, every color, every second of a music video, every web page, and every software. This is base 2 numbering, and as programmers, we need to grasp how this works if we intend to connect with these computers effectively. So in this article we will focus on how convert from hex to binary?
What Is the Hex to Binary Conversion?
Hexadecimal to binary conversion is to find the binary equivalent of the hexadécimal number. We will talk about a change from a base 16 to a base 2.
In the same perspective the representation that everyone knows and that is in everyday life is the decimal representation in the base 10 (0,1,2,3,…), whereas the base 16 (hex) and the base 2 (binary) is the one that is understood and interpretable by the machine (the computer), which derives from the electronic design of the computer that includes only the 0 or the 1, in reference to the electronic component transistor, which is a kind of a power switch ON/OFF or 0/1:
0: no current (0v) and 1: current presence (3.3v/5v)
What is a Hexadecimal Number System?
As explained earlier, the hexadecimal representation is a representation formed by two parts called (digits) each of which uses a symbol among the following: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F
What is a Binary Number System?
A binary representation is a sequence formed only by a symbol called a bit whose value is: 0 or 1.
Hex to Binary Conversion Table
| Hexadecimal | Decimal | Binary |
| 0 | 0 | 00000000 |
| 1 | 1 | 00000001 |
| 2 | 2 | 00000010 |
| 3 | 3 | 00000011 |
| 4 | 4 | 00000100 |
| 5 | 5 | 00000101 |
| 6 | 6 | 00000110 |
| 7 | 7 | 00000111 |
| 8 | 8 | 00001000 |
| 9 | 9 | 00001001 |
| A | 10 | 00001010 |
| B | 11 | 00001011 |
| C | 12 | 00001100 |
| D | 13 | 00001101 |
| E | 14 | 00001110 |
| F | 15 | 00001111 |
How to Convert from Hex to Binary Number?
To convert a hex number to a binary number, just follow these steps:
How to convert directly from hexadecimal to binary?
To do the direct conversion, we take each digits in the hexadecimal number and do conversion using the table above. and the concatenate the to digits:
(1A)h = 1 A
= 0001 1010
= (00011010)b → also we can represent it like this: (11010)bHow to convert indirectly from hexadecimal to binary?
Step 1: Locate each digit forming the hex number and multiply each digit by 16p-1 where p represents the position of the digit.
Step 2: Sum all of the items you have multiplied
Step 3: The sum obtained is the decimal representation of our hexadecimal number that we will convert to binary:
Step 4: Divide the decimal sum by two
Step 5: Note the rest of the division. And divide the result again if it is different from zero.
Step 6: Repeat step 5 until a zero result is obtained.
Step 7: Recover all the remains starting with the last one and put it to the right (most significant bit).By following these steps described above, you will get a result of the conversion of a hex number into a binary number by going through an intermediate conversion (in decimal of the number).
Examples of How Convert from Hex to Binary
- Example 1: Convert (F)h to a binary number.
First we will convert our hex (F)h to a decimal number:
(F)h = (F x 16^0)
= (15 x 16^0)
= (15 x 1)
= 15
= (15)dNext, you have to convert the previously obtained number into a binary number:
(250)d = 15 / 2 → 1
= 7 / 2 → 1
= 3 / 2 → 1
= 1 / 2 → 1 stops the result is zero
So the result is: (1111)b- Example 2: Convert (FA)h to a binary number.
First we will convert our hex (FA)h to a decimal number:
(FA)h = (F x 161) + (A x 160)
= (15 x 161) + (10 x 160)
= (15 x 16) + (10 x 1)
= 240 + 10
= (250)dNext, you have to convert the previously obtained number into a binary number:
(250)d = 250 / 2 → 0
= 125 / 2 → 1
= 62 / 2 → 0
= 31 / 2 → 1
= 15 / 2 → 1
= 7 / 2 → 1
= 3 / 2 → 1
= 1 / 2 → 1 stops the result is zero
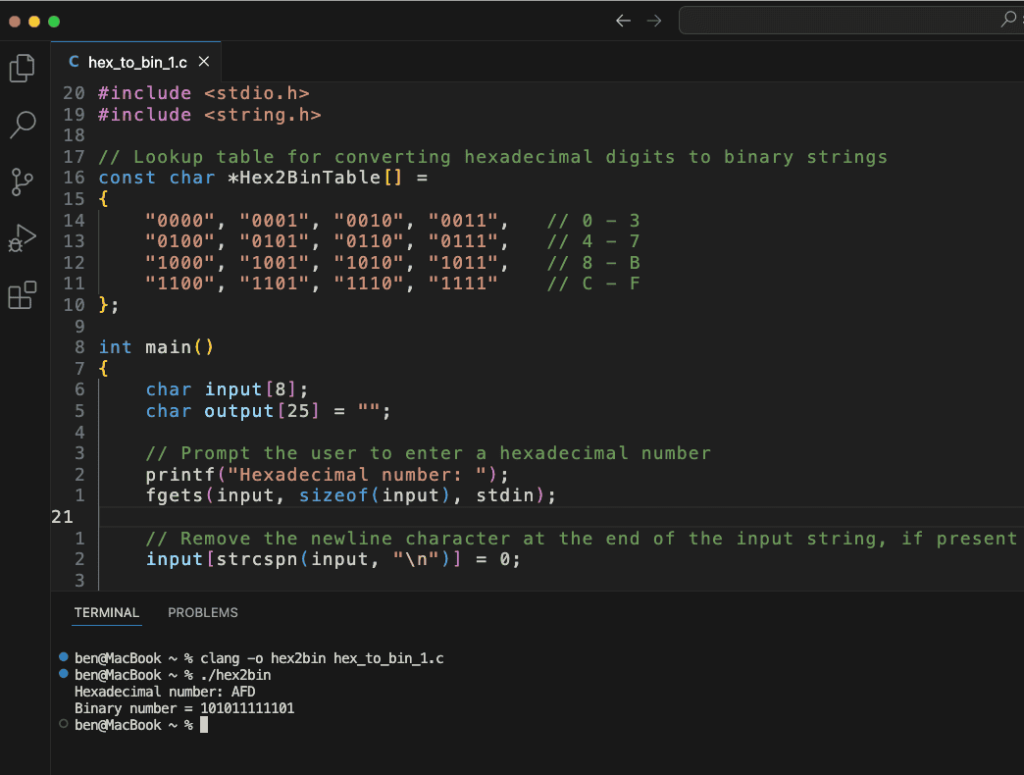
So the result is: (11111010)bC Program to Convert Hexadecimal to Binary number
Hereafter a two programs written in c langage that convert from hex to binary number, this program will take as input the hex number and will give a binary representation number as output:
#include <stdio.h>
#include <string.h>
// Lookup table for converting hexadecimal digits to binary strings
const char *Hex2BinTable[] =
{
"0000", "0001", "0010", "0011", // 0 - 3
"0100", "0101", "0110", "0111", // 4 - 7
"1000", "1001", "1010", "1011", // 8 - B
"1100", "1101", "1110", "1111" // C - F
};
int main()
{
char input[8];
char output[25] = "";
// Prompt the user to enter a hexadecimal number
printf("Hexadecimal number: ");
fgets(input, sizeof(input), stdin);
// Remove the newline character at the end of the input string
input[strcspn(input, "\n")] = 0;
// Loop through each character in the input string
for (int i = 0; input[i] != '\0'; i++)
{
// Calculate the numeric value of the current hexadecimal digit
int val = input[i] - (input[i] >= 'A' ? (input[i] >= 'a' ? 'a' - 10 : 'A' - 10) : '0');
// If the value is valid (0-15), append the corresponding binary
if (val >= 0 && val <= 15)
strcat(output, Hex2BinTable[val]);
else
{
// print an error and exit
printf("Invalid hexadecimal digit %c\n", input[i]);
return 1;
}
}
// Show the conversion result
printf("Binary number = %s\n", output);
return 0;
}
Some Problems to Practice
- Convert (55AA) to an equivalent binary number
- Convert (28C) to an equivalent binary number
- Convert (D5) to an equivalent binary number
- Convert (200) to an equivalent binary number
Questions Frequently Asked
Hereafter some of the most frequently asked questions about how to convert a hex number to a binary number
- Hexadecimal and binary: What differences and conversion methods?
- What’s Binary representation of hexadecimal “AA”?
- What’s Binary equivalent to hexadecimal?
- How to convert all hexadecimal digits to binaries?
- History of the use of hexadecimal in calculation (Binary representation)?
- What Binary representation of the hexadecimal value “1F”?
- How to check the correctness of the hexadecimal to binary conversion?
- What kind of Tool to use in hexa to binary conversion?
Conclusion
it's crazy how from these two binary values '0‘ or ‘1‘ the computer manages to make all the renderings that we can see: images, videos, sounds, 3d video games, virtual reality with interaction with sensors, camera and all the computing power to send space shuttles with astronauts to the moon or almost 😉





